III Simulation Methods and Boundary Conditions
A Multicanonical Monte-Carlo (MCMC) Simulation
[69.2.2.1] Monte Carlo (MC) simulations with simple sampling (SS) probe configurations
according to their geometrical multiplicity and re-weight them with their
thermodynamic probability ![]() , so for an observable
, so for an observable ![]() the
average is computed as
the
average is computed as
| (13) |
[page 70, §0] [70.1.0.1] Standard importance sampling (IS) methods like the Metropolis-algorithm accept and reject configurations according to their relative thermodynamic probability, so that the thermodynamic weight is built into the sampling process instead of the re-weighting, and therefore the thermodynamic average reduces to a simple average
| (14) |
[70.1.0.2] In some cases, Metropolis-type sampling can be inefficient because some
configurations may be ”rare” with respect to their thermodynamic weight, but
”important” because their contribution ![]() is disproportionately large,
or because the range with small probability contains a ”barrier” to cross so
that other, more ”important” configurations can be reached.
[70.1.0.3] To overcome this problem of sampling ”rare events”, Berg and Neuhaus [26] proposed a
method that modifies the importance sampling procedure in such a way that
”artificial” probabilities
is disproportionately large,
or because the range with small probability contains a ”barrier” to cross so
that other, more ”important” configurations can be reached.
[70.1.0.3] To overcome this problem of sampling ”rare events”, Berg and Neuhaus [26] proposed a
method that modifies the importance sampling procedure in such a way that
”artificial” probabilities ![]() are introduced for each
are introduced for each ![]() . Because not
a single canonical sampling is used, but each observable lives on it’s ”own”
canonical average, the method was called ”multi-canonical Monte Carlo” (MCMC).
[70.1.0.4] The Metropolis-type averages of eq. (14) are then modified to
. Because not
a single canonical sampling is used, but each observable lives on it’s ”own”
canonical average, the method was called ”multi-canonical Monte Carlo” (MCMC).
[70.1.0.4] The Metropolis-type averages of eq. (14) are then modified to
| (15) |
[70.1.0.5] The weights ![]() can be chosen for convenience,
e.g. in such a way that all
can be chosen for convenience,
e.g. in such a way that all ![]() are sampled uniformly, or some part of the phase space is sampled with higher
frequency than another part [27].
are sampled uniformly, or some part of the phase space is sampled with higher
frequency than another part [27].
B Implementation
[70.1.1.1] We implemented a Monte-Carlo algorithm on a square grid with Glauber
dynamics. The grid has an even number of sites in each direction, so
that we can use the checker-board update scheme, which has the
smallest correlation time [28] under all single-spin
update-schemes in the straightforward Metropolis-algorithm.
[70.1.1.2] Our Fortran ![]() program using sub-arrays allowed a simple implementation
of fixed or periodic boundaries. We choose not to implement
bit-coding, as the bulk of the computer time would be spent in
updating the information of the MCMC-procedure rather than for the
straightforward algorithm.
[70.1.1.3] The implementation using non-overlapping sub-arrays also allows vectorization.
[70.1.1.4] In addition we parallelized the algorithm.
program using sub-arrays allowed a simple implementation
of fixed or periodic boundaries. We choose not to implement
bit-coding, as the bulk of the computer time would be spent in
updating the information of the MCMC-procedure rather than for the
straightforward algorithm.
[70.1.1.3] The implementation using non-overlapping sub-arrays also allows vectorization.
[70.1.1.4] In addition we parallelized the algorithm.
[70.1.2.1] To sample the magnetizations evenly, theweights ![]() in eq. (15)
is chosen according to the magnetization,
in eq. (15)
is chosen according to the magnetization,
![]() The MCMC proceeds in several iterations
The MCMC proceeds in several iterations ![]() , during
which the intermediate
, during
which the intermediate ![]() are consecutively refined using the
previously computed entries so that
are consecutively refined using the
previously computed entries so that ![]() are obtained.
[70.1.2.2] Probabilities
are obtained.
[70.1.2.2] Probabilities ![]() are evaluated from the histogram
of the visited magnetizations during each spin update.
[70.1.2.3] Details of our algorithm for the magnetization distribution will be published elsewhere.
are evaluated from the histogram
of the visited magnetizations during each spin update.
[70.1.2.3] Details of our algorithm for the magnetization distribution will be published elsewhere.
C Convergence
[70.2.1.1] The objective of our Monte-Carlo simulations is to obtain information
about the equilibrium states (i.e. long time limit) for an infinite
system (i.e. large ![]() limit).
limit).
[70.2.2.1] We must distinguish between two kinds of convergence:
MCS-convergence: By this we mean that, at given
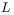 and
and 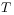 ,
the individual simulation run is converged in the sense that
increasing the number of Monte-Carlo steps (MCS) will not change the
order parameter distribution. The measured distribution is the
“true” distribution for the given system size and temperature.
,
the individual simulation run is converged in the sense that
increasing the number of Monte-Carlo steps (MCS) will not change the
order parameter distribution. The measured distribution is the
“true” distribution for the given system size and temperature.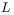 -convergence: By this we mean the convergence of the
distribution with
-convergence: By this we mean the convergence of the
distribution with 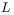 at given
at given 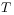 to its form for the infinite
system.
to its form for the infinite
system.
[70.2.3.1] The autocorrelation time needed by the algorithm to go from large negative magnetizations to large positive magnetizations increases rapidly as the system size becomes large. [70.2.4.1] Therefore it is difficult to obtain fully MCS-converged results at large system sizes. [70.2.4.2] Because we are interested only in the tail behaviour we need to exclude all cutoffs not resulting from the system size, and hence need fully MCS-converged results.
[70.2.5.1] Within available resources and with simulation for ![]() Monte Carlo
steps per iteration and
Monte Carlo
steps per iteration and ![]() multicanonical iterations on a Cray-T3E
with
multicanonical iterations on a Cray-T3E
with ![]() processors we could obtain statistics all the way up to the
saturation magnetization for system sizes
processors we could obtain statistics all the way up to the
saturation magnetization for system sizes ![]() .
[70.2.5.2] Simulations for
.
[70.2.5.2] Simulations for ![]() did not MCS-converge fully within the available computer time.
[70.2.5.3] For
did not MCS-converge fully within the available computer time.
[70.2.5.3] For ![]() the simulation runs do not reach
the simulation runs do not reach ![]() , and
achieve statistics only upto
, and
achieve statistics only upto ![]() .
[70.2.5.4] Although this is a significant improvement over the tails statistics presented in
Ref. [9], it is still not sufficient for our tail analysis.
[70.2.5.5] Therefore our results below are limited to system sizes
.
[70.2.5.4] Although this is a significant improvement over the tails statistics presented in
Ref. [9], it is still not sufficient for our tail analysis.
[70.2.5.5] Therefore our results below are limited to system sizes ![]() .
.
D Far tail regime
[70.2.6.1] MCMC simulations of the two-dimensional Ising model provide far better statistics in the tails than the Swendsen-Wang cluster flip algorithm [9]. [70.2.6.2] As discussed in Section II adequate statistics is required in the “far tail regime” close and prior to saturated magnetization. [70.2.6.3] This regime is defined as
| (16) |
where ![]() is the magnetization per spin and
is the magnetization per spin and ![]() is the most probable magnetization.
[70.2.6.4] We define the position of the (local or global) maxima of
is the most probable magnetization.
[70.2.6.4] We define the position of the (local or global) maxima of ![]() as the most probable magnetization
denoted by
as the most probable magnetization
denoted by ![]() .
[70.2.6.5] For the scaling variable defined in eq. (9) this implies
.
[70.2.6.5] For the scaling variable defined in eq. (9) this implies
| (17) |
[page 71, §1]
E Boundary Conditions
[71.1.1.1] Most previous investigations have concen-trated on periodic boundary conditions.
[71.1.1.2] These boundary conditions have the advantage of preserving the fundamental symmetry.
[71.1.1.3] In this paper we present also results for fixed symmetry breaking boundary conditions
where all boundary spins are fixed to ![]() .
.
[71.1.2.1] Our motivation for investigating fixed boundary conditions comes from Ref. [23]. In particular one expects that the order parameter distribution becomes asymmetric, and this raises the question whether or not the left and the right tail behave in the same way.
