1 Introduction and Statement of the Problem
[page 1, §1]
[1.2.1.1] A recent classification theory [1, 2, 3] has derived
fractional equations of motion from abstract ergodic theory.
[1.2.1.2] Fractional
equations of motion contain fractional rather than integer order time
derivatives as generators of the time evolution.
[1.2.1.3] Fractional equations
of motion arise at anequilibrium phase transitions [1, 2]
or whenever a dynamical system is restricted to subsets of measure zero
of its state space [3].
[1.2.2.1] Master equations in which the time derivative is replaced with a
derivative of fractional order form the subject of the present paper.
[1.2.2.2] Such fractional master equations arise as special cases of the
more general fractional Liouville equation introduced in
[1, 2, 3], and they contain the fractional
diffusion equation as a special case.
[1.2.2.3] A fractional master equation
for a translationally invariant ![]() -dimensional system may be written
formally, but in suggestive notation, as
-dimensional system may be written
formally, but in suggestive notation, as
| (1.1) |
where ![]() denotes the probability density to find the
diffusing entity at the position
denotes the probability density to find the
diffusing entity at the position ![]() at time
at time ![]() if it was at the origin
if it was at the origin ![]() at time
at time ![]() .
[1.2.2.4] The positions
.
[1.2.2.4] The positions ![]() may be discrete or continuous.
[1.2.2.5] The fractional
transition rates
may be discrete or continuous.
[1.2.2.5] The fractional
transition rates ![]() measure the propensity for a
displacement
measure the propensity for a
displacement ![]() in units of (1/time
in units of (1/time![]() , and obey the
relation
, and obey the
relation ![]() .
[1.2.2.6] The fractional order
.
[1.2.2.6] The fractional order ![]() plays the role of a dynamical critical exponent.
[1.2.2.7] Equation
(1.1) can be made precise
by applying the fractional Riemann-Liouville integral as
plays the role of a dynamical critical exponent.
[1.2.2.7] Equation
(1.1) can be made precise
by applying the fractional Riemann-Liouville integral as
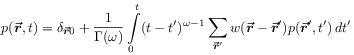 |
(1.2) |
where the initial condition ![]() has been
incorporated.
has been
incorporated.
[1.3.1.1] Diffusion in a ![]() -dimensional euclidean space is contained
in the fractional master equations (1.1) or (1.2)
as the special case in which
-dimensional euclidean space is contained
in the fractional master equations (1.1) or (1.2)
as the special case in which ![]() and
and ![]() is the
discretized Laplacian on a
is the
discretized Laplacian on a ![]() -dimensional regular lattice.
[1.3.1.2] The integral form (1.2) suggests a relation with the
well known theory of continuous time random walks
[4, 5, 6, 7, 8, 9, 10].
[1.3.1.3] It is the purpose and
objective of the present paper to show that there exists a
precise and rigorous relation between the fractional master
equation and the theory of continuous time random walks.
[1.3.1.4] It will be shown that the fractional master equation describes
a fractal time process [11, 10].
[1.3.1.5] Fractal time processes
(see [10] for a review) are defined here as continuous
time random walks whose waiting time density has an infinite
first moment [12, 13, 14, 15, 16].
-dimensional regular lattice.
[1.3.1.2] The integral form (1.2) suggests a relation with the
well known theory of continuous time random walks
[4, 5, 6, 7, 8, 9, 10].
[1.3.1.3] It is the purpose and
objective of the present paper to show that there exists a
precise and rigorous relation between the fractional master
equation and the theory of continuous time random walks.
[1.3.1.4] It will be shown that the fractional master equation describes
a fractal time process [11, 10].
[1.3.1.5] Fractal time processes
(see [10] for a review) are defined here as continuous
time random walks whose waiting time density has an infinite
first moment [12, 13, 14, 15, 16].
[1.3.2.1] Given the existence of an exact relation between fractional
master equations and fractal time random walks, it might seem
that (1.1) or (1.2) describe also diffusion on
fractals.
[1.3.2.2] Dimensional analysis suggests anomalous subdiffusive
behaviour of the form![]() where
where ![]() is the fractal dimension, and
is the fractal dimension, and ![]() is the spectral or fracton dimension [17, 18, 19], and
indeed some authors have suggested that
is the spectral or fracton dimension [17, 18, 19], and
indeed some authors have suggested that ![]() .
[1.3.2.3] It must be clear however, that while the relation between fractional
master equations and fractal time random walks established in this
paper is exact, the relation with diffusion on fractals is not.
[1.3.2.4] It appears doubtful that the latter relation can exist beyond
superficial scaling similarities because exactly solvable cases
show that the spectral properties as well as the eigenfunctions
for fractal time walks and walks on fractals are radically
different [20, 21, 22, 23].
.
[1.3.2.3] It must be clear however, that while the relation between fractional
master equations and fractal time random walks established in this
paper is exact, the relation with diffusion on fractals is not.
[1.3.2.4] It appears doubtful that the latter relation can exist beyond
superficial scaling similarities because exactly solvable cases
show that the spectral properties as well as the eigenfunctions
for fractal time walks and walks on fractals are radically
different [20, 21, 22, 23].
